Alvaro VidelaRead my Thoughts. Follow my Leads.

Java ThreadLocalRandom Explained

October 26 2016

In this blogpost I’d like to present some things I’ve found while trying to understand the implementation of the jdk8 ThreadLocalRandom class. What was my motivation for doing something like that? Over the weekend I was reading the Second Volume from Knuth’s TAOCP “Seminumerical Algorithms”, where he devotes the whole of Chapter 3 describing techniques for generating random numbers with a computer, and then explaining how to test those random number generators (of couse we are talking about pseudo random number generators or PRNGs). Near the end of the chapter Knuth proposes the following exercise:

Look at the subroutine library of each computer installation in your organization, and replace the random number generators by good ones. Try to avoid being too shocked at what you find.

That seemed like a good exercise, but while I didn’t want to replace the PRNGs on my organisation, I decided to take a look at the implementation and see for myself. I grabbed the code from OpenJDK and went straight to check the implementation of ThreadLocalRandom. The class ThreadLocalRandom (TLR from now on), is an implementation of the interface offered by the Random class. Random is an implementation of the Linear Congruence Method presented by Knuth on TAOCP. A quick foray into TLR revealed something totally different.

In trying to understand TLR, I downloaded the source code for the class, and got it into IntelliJ. I tried to just ignore the comments, and go and read the code as is. What an interesting experience! The code is full of hardcoded constants like the following:

private static int mix32(long z) {
    z = (z ^ (z >>> 33)) * 0xff51afd7ed558ccdL;
    return (int)(((z ^ (z >>> 33)) * 0xc4ceb9fe1a85ec53L) >>> 32);
}

What is 0xff51afd7ed558ccdL or 0xc4ceb9fe1a85ec53L? How do they come up with those constants? And there’s even a couple more:

0x9e3779b97f4a7c15L
0x9e3779b9
0xbb67ae8584caa73bL

A little googling revealed that 0x9e3779b97f4a7c15L and 0x9e3779b9 come from The R5 Encryption Algorithm by Rivest (the same person that gave the R to RSA). In the paper we can see that Rivest took the Golden Ratio number and used it in the following formula to produce either 0x9e3779b97f4a7c15L or 0x9e3779b9:

Q = Odd((φ - 1)2^w)

Where Odd is a function that returns the nearest integer to the input parameter. Then w is the wordsize we want to use, like 32 or 64. As you might have guessed 0x9e3779b97f4a7c15L is the 64bit version of the constant and 0x9e3779b9 is the 32bit version. Note that 0x9e3779b9 is also used in the Tiny Encryption Algorithm.

The constant 0x9e3779b97f4a7c15L is called GAMMA in the TLR source code and 0x9e3779b9 is called PROBE_INCREMENT.

Then we have 0xbb67ae8584caa73bL which in TLR is called SEEDER_INCREMENT. That one is easier, since it’s just the fractional part of the square root of 3 obtained like this:

frac(sqrt(3)) * 2^64

It happens that that constant is used in the SHA512 algorithm, which does a similar procedure to the first 8 prime numbers to extract 8 constants that are used in the algorithm as well.

Then we have 0xff51afd7ed558ccdL and 0xc4ceb9fe1a85ec53L which are used in the mix32 method shown above. Google reveals that these constants come from the finaliser step of the MurmurHash3 algorithm.

So far so good, but what are all these numbers used for. To understand this, we need to understand what’s the purpose of ThreadLocalRandom. As the name suggest, the idea is to have a source of random numbers, per thread, so we can obtain random numbers concurrently. This means that every time a thread initialises an instance of TLR, the code needs to initialise the random seed for that particular thread. The seed is initialised on a mixed version of SEEDER_INCREMENT; at the same time, a PROBE value is initialised for that particular thread by adding the PROBE_INCREMENT to the current probeGenerator value. What’s that probe value used for? It is used by classes like ConcurrentHashMap to calculate hashes for the map keys.

So we have constants taken from RC5 and TEA, SHA512 and MurmurHash3. This is starting to make no sense at all, but let’s check how it all works when put together to see if we can make sense out of this.

Obtaining Random Numbers

To get a random number from ThreadLocalRandom we can call the method nextInt() which is part of the interface exposed by Random as well. Let’s check the implementation of that method:

public int nextInt() {
    return mix32(nextSeed());
}

So we compute the next seed and that’s mixed and returned to the user. Let’s see what nextSeed() is doing:

final long nextSeed() {
    Thread t; long r; // read and update per-thread seed
    UNSAFE.putLong(t = Thread.currentThread(), SEED,
                   r = UNSAFE.getLong(t, SEED) + GAMMA);
    return r;
}

That method obtains the current value of the seed and just adds to it the value of the GAMMA constant presented above. This doesn’t look random at all, for some defintion of the word random anyway. If we go back to Knuth, the Linear Congruence Method proposed in his book involves a calculation like this:

nextseed = (oldseed * multiplier + addend) & mask;

So we have a multiplier, and addend, and then we apply a mask to that value.

The method used by TLR lacks the multiplier part but in TAOCP Knuth is very clear that the lack of multiplier has the effect of producing a sequence that’s “everything but random”. The TLR case is like setting the multiplier to 1 in the Linear Congruence Method.

So there’s either something very wrong with ThreadLocalRandom or I am missing something. Considering that ThreadLocalRandom is part of the JDK used by millions of developers, I’m pretty sure that I am at fault, and I’m for sure missing something. Time to read those comments.

Right at the top of the class we have this comment:

Even though this class subclasses java.util.Random, it uses the same basic algorithm as java.util.SplittableRandom.

So let’s check SplittableRandom and see what we find out over there, but this time let’s read the comments there as well.

The Theory Behind ThreadLocalRandom

When we open SplittableRandom’s sourcecode we find this illustrative comment:

/*
 * This algorithm was inspired by the "DotMix" algorithm by
 * Leiserson, Schardl, and Sukha "Deterministic Parallel
 * Random-Number Generation for Dynamic-Multithreading Platforms",
 * PPoPP 2012, as well as those in "Parallel random numbers: as
 * easy as 1, 2, 3" by Salmon, Morae, Dror, and Shaw, SC 2011.  It
 * differs mainly in simplifying and cheapening operations.
 */

Here’s the paper Deterministic Parallel Random-Number Generation for Dynamic-Multithreading Platforms and here we have Parallel random numbers: as easy as 1, 2, 3.

The goal of the first paper by Leiserson, Schardl, and Sukha (from now on LSS) is to see how to create an efficient Deterministic parallel random-number generators for dthreading platforms (as opposed to POSIX’s pthreading). Dthreading is an implementation of the Fork-Join parallel computation model. The problem is that traditional DPRNGs don’t scale to hundreds of thousands of strands (read green-threads), since they were made with the pthread model in mind. In that paper they present an algorithm for DPRNGs called DotMix, which uses a dot product of a pedigree and then mixes the result using the RC6 algorithm. They claim DotMix has a statistic quality which rivals the one from the Mersenne Twister algorithm and should work for hundreds of thousands of strands.

What they mean by saying those other algorithms don’t scale? The problem of parallel streams of random numbers is that there has to be some way to prevent two streams from producing the same sequence of random numbers. We could keep state around and synchronise using locks among threads, but that will be slow. They are trying to find a way for each thread to be able to have a seed for their random numbers that doesn’t depend on shared state.

What’s a Pedigree?

They use the following definition to explain a pedigree which if we don’t read the original paper, it won’t make much sense:

A pedigree scheme uniquely identifies each strand of a dthreaded program in a scheduler-independent manner.

Let’s try to understand that definition in the context of a fork-join parallel computing model. Each thread can fork multiple threads by calling fork (spawn in the LSS paper), or could generate a value. At the same time the spawned threads can also do the same: either spawn a new child thread or generate more values. Now let’s represent that model using the following tree:

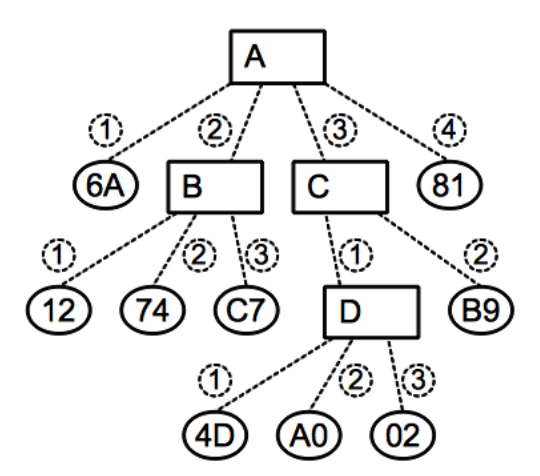
fork-join-tree

We have that the root task A generated the value 6A, forked the thread B and then C, and generated 81. Then the task B generated three values: 12, 74 and C7. Then C forked D and generated B9; and so on.

An oversimplification of what LSS claims is that the pedigree of each value, taken as the vector of labels in the tree from the generated value leaf to the root, is unique, independently of the scheduling of the tasks. For example the value 74 has the following pedigree: <2, 2>.

We have a unique vector per thread, but how do we generate Random Numbers from there? The authors of DotMix talk about the idea of compressing the values of the vector to a single machine word. Here’s were the Dot part of DotMix comes into play. They calculate the dot product of the pedigree vector with another vector of integers “chosen uniformly at random” (see they paper for the exact details).

This integer hash that’s produced from the dot product has a small probability of collision with the ones produced by other threads. The problem is that now two similar pedigrees can produce similar hashes, but the authors of DotMix wanted the produced value to be statistically dissimilar from other hashes. To solve that problem they introduced the mixing part to DotMix. So, what’s mixing?

What’s Mixing?

The mixing step of the algorithm applies a function to the hash value obtained from the pedigree in order to reduce the statistical correlation of two hash values, so it becomes hard to predict their sequence. In the case of DotMix, the mix function swaps the high and low order bits of the hash value, that is, a function that in a 64bit hash for example, swaps the first 32bit part with the second one. For DotMix they use a mixing function based on the RC6 Encryption Algorithm.

Counter Based PRNGs

From the description of DotMix we can see that ThreadLocalRandom is using a mixing step that’s applied to the seed obtained from nextSeed, but as we saw nextSeed just increases the currentSeed by the value of the GAMMA constant, which means this has nothing to do with pedigrees. Here’s where the other paper mentioned in the comments comes into play.

The paper “Parallel random numbers: as easy as 1, 2, 3” by Salmon, Morae, Dror, and Shaw presents the idea of Counter Based PRNGs. In their paper they are trying to solve the problem of having “massively parallel high-performance computations”, for which they say traditional PRNGs don’t scale well.

The problem with traditional PRNGs like the method from TAOCP is that they are serial. So to calculate random number N+1 we need to have calculated the Nth random number before. If we want to produce several streams of random numbers, then that approach won’t scale if our goal is to be sure the streams are different, since initialising each stream with its own seed becomes complicated.

To counter that problem they propose a simple function to produce a sequence of numbers:

f(s) = (s + 1) mod 2^p

That function is just a simple counter that increases the input value by one and then applies mod to some power of two. Since it’s just a counter, this method is called Counter Based PRNGs.

At this point we might start hurting our own eye muscles from so much eye-rolling but stay with me. The counter function could use just 1 as the increment as in that example or use a number a bit more complicated like the GAMMA value used in ThreadLocalRandom. Still, we don’t have random numbers yet.

What the authors of that paper propose is that we apply a cryptographically secure function to the values produced by the counter function. In particular they propose using parts of AES or Threefish to the value produced by the counter. In their paper instead of incrementing the counter by 1 they propose a couple of constants that are also used in ThreadLocalRandom: 0xbb67ae8584caa73b and 0x9e3779b97f4a7c15 which are our SEEDER_INCREMENT and GAMMA values mentioned before. They say that by using these constants and some variants of AES or Threefish they managed to pass the TestU01’s BigCrush tests for PRNGs and their PRNGs produce periods of 2^128 numbers.

Getting the Puzzle Together

So now we are managing to put together the puzzle of ThreadLocalRandom. From DotMix we have the mixing function and from Salmon et al. we get the idea of Counter-Based PRNGs. There’s still a missing piece though: why is ThreadLocalRandom using what seems to be a custom mixing function?

It happens that ThreadLocalRandom mix32 and mix64 are not custom at all. They are in fact based on MurmurHash3 finaliser function. The idea behind that function is to produce an Avalanche Effect on the bits of the value passed to the mix function. The Avalanche Effect is a technique that by flipping a single bit, manages to change enough bits (the avalanche part) so that the resulting number is quite different from the input. So if we pass two values to the function that are quite similar, the mixing function will make sure they end up quite different. If we look at mix32 again we will see a couple of constants there, 0xff51afd7ed558ccdL and 0xc4ceb9fe1a85ec53L.

private static int mix32(long z) {
    z = (z ^ (z >>> 33)) * 0xff51afd7ed558ccdL;
    return (int)(((z ^ (z >>> 33)) * 0xc4ceb9fe1a85ec53L) >>> 32);
}

According to the creator of MurmurHash3 these constants were chosen because they produce an Avalanche Effect with a probability near to 0.5, but the story does not end here. SplittableRandom does not use the same constants!

// SplittableRandom implementation
private static long mix64(long z) {
    z = (z ^ (z >>> 30)) * 0xbf58476d1ce4e5b9L;
    z = (z ^ (z >>> 27)) * 0x94d049bb133111ebL;
    return z ^ (z >>> 31);
}

The constants used here were suggested by David Stafford in his blog who found them after running some experiments. For some reason SplittableRandom has the better constants while ThreadLocalRandom does not.

ThreadLocalRandom a Random Algorithm?

One thing that Knuth tries to make clear in his book is that we should not use a random algorithm to produce a PRNGs. That is, the steps of the algorithm shouldn’t be chosen at random, like grab a piece from here, another from there, put them together, shake it a bit, and TAH DAH! we got a PRNG. So far this seems to be the case with ThreadLocalRandom. What are we missing?

There’s yet another paper called Fast Splittable Pseudorandom Number Generators. Its authors are Guy Steele, Doug Lea and Christine H. Flood, which in case you don’t know, they are all people involved with the development of the JDK. What is that paper about? It explains the algorithm behind SplittableRandom, which is the one used for ThreadLocalRandom as well (with some small diferences as explained above).

In that paper they explain that they took DotMix and implemented it in Scala because the language would permit them a clean implementation which they could analyse for further improvements which then would be translated to Java. That’s a pretty interesting use case for Scala.

Once they had DotMix implemented they tried to refine it, focusing on simplifying it’s steps, trying to increase the performance of the algorithm, while at the same time keeping it secure enough to pass the TestU01 battery of tests. So a pedigree based PRNG became a counter based one; and cryptographically secure for mixing (but arguably slow) functions for mixing became the finaliser function from MurmurHash3. Of course they put their new PRNG algorithm under the battery of tests offered by TestU01 which is the industry standard for testing PRNGs.

There’s a historical note from that paper that it’s worth noticing. The paper is from October 2014. On December that year a paper from INRIA got submitted for publication which discussed the MRG32k3a algorithm as a way to replace ThreadLocalRandom implementation. If we read Steele’s et al paper we see that they reviewed MRG32k3a but they saw it didn’t fit their selection criteria, because it wouldn’t allow to split the stream beyond 192 sub-threads. I would assume that the authors of the INRIA paper didn’t know about Steele’s paper at the time of publication.

Another interesting note from that paper is their commentary on Haskell’s System.Random implementation:

The API is beautiful; the implementation turns out to have a severe flaw.

Conclusion

On this interesting journey through ThreadLocalRandom we saw that while we found quite a few things along the way that seemed to have no logical explanation, there was in fact a reason for them to be there. In this case the authors of ThreadLocalRandom took two algorithms for producing PRNGs and refined their implementation until they reached to what SplittableRandom is (and subsequently ThreadLocalRandom). Even if that method seems sound, a PRNG needs testing of its statistical properties, and Steele et al tell us that their SplitMix passes the TestU01 battery of tests.

Credits

The fork-join tree image and the explanation comes from the paper by Guy Steele et al mentioned above.

blog comments powered by Disqus